Consiste en cambiar la amplitud de la sinusoide entre dos valores posibles; si uno de los valores es cero se le llama OOK (On-Off keying). La aplicación más popular de ASK son las transmisiones con fibra óptica ya que es muy fácil "prender" y "apagar" el haz de luz; además la fibra soporta las desventajas de los métodos de modulación de amplitud ya que posee poca atenuación. Otra aplicación es el cable transoceánico.
El modulador es un simple multiplicador de los datos binarios por la portadora. A continuación se ilustra un ejemplo de un mensaje en banda base y el resultado de modular en ASK(OOK).
ASK puede ser definido como un sistema con una señal para el "1" igual a s1(t)= Sinusoide y una señal para el cero igual a s0(t) = 0.
Definamos una señal b(t) que toma el valor de 1 cuando el bit enviado es un “1”lógico y –1 cuando el bit enviado es un “0”.
La señal ASK puede expresarse como:
Como se observa b(t) es una onda NRZ polar, por lo tanto su espectro, que es infinito, quedará trasladado a fc . Como el espectro de b(t) es un Sinc 2 con cortes cada fb=1/tb, y como siempre se elige fc mucho mayor que fb, entonces el espectro de la señal ASK quedará:
Si integramos esta DEP encontraremos que la potencia resulta V2 /4
Se observa que el ancho de banda práctico es 2fb el cual es el doble del requerido en transmisión banda base. Otro parámetro que será muy útil sobre todo en modulación multinivel es la constelación que a continuación definiremos:
La constelación consiste en representar la señal modulada en función de una o varias funciones ortonormales (ortogonales de energía unitaria). En este caso, como uno de los símbolos es nulo queda claro que existe una sola base que es una sinusoide. Esa base debe tener energía unitaria.
El resultado obtenido para la base es considerando que fc = nfb , es decir la frecuencia de ortadora es múltiplo entero de tb (en tb cabe un número entero de ciclos de la sinusoide).
La distancia entre los posibles símbolos es muy importante, ya que representará la fortaleza que tiene la modulación frente al ruido. Observe que si los símbolos están más distanciados, será mas difícil que uno se convierta en otro por efectos del ruido añadido en el sistema.
7.2 PSK: Modulación digital de fase
Aunque PSK no es usado directamente hoy en día, es la base para entender otros sistemas de modulación de fase multinivel. Consiste en variar la fase de la sinusoide de acuerdo a los datos. Para el caso binario, las fases que se seleccionan son 0 y π. En este caso la modulación de fase recibe el nombre de PRK (Phase Reversal Keying). Observe, en la siguiente figura, una señal PRK:
La expresión temporal de esta señal, en función de una señal binaria b(t) NRZp sería
La densidad espectral de potencia DEP de la señal PRK viene dada por:
El espectro es parecido al de ASK solo que no incluye las deltas de Dirac. Esto implica un ahorro de potencia. El ancho de banda resulta igual al de ASK o sea 2fb.
Su constelación final es:
7.3 Modulación de amplitud en cuadratura (QAM)
La Modulación de amplitud en cuadratura (conocida
también como QAM por las siglas en inglés de Quadrature amplitude modulation) es una técnica que transporta datos, mediante la modulación de la señal portadora, tanto en amplitud como en fase. Esto
se consigue modulando una misma portadora, desfasada en 90°. La señal modulada
en QAM está compuesta por la suma lineal de dos señales previamente moduladas
en Doble Banda
Lateral con Portadora Suprimida.
Se asocian a esta tecnología
aplicaciones tales como:
- Modems telefónicos para velocidades superiores a los 2400bps.
- Transmisión de señales de televisión, microondas, satélite (datos a alta velocidad por canales con ancho de banda restringido).
- Modulación TCM (Trellis Coded Modulation), que consigue velocidades de transmisión muy elevadas combinando la modulación con la codificación de canal.
- Módems ADSL que trabajan en el bucle de abonado, a frecuencias situadas entre 24KHz y 1104KHz, pudiendo obtener velocidades de datos de hasta 9Mbps, modulando en QAM diferentes portadoras.
Diagramas moduladores y demoduladores
Modulador analógico: Las
señales de entrada I(t) y Q(t), pasan por moduladores de producto que
modulan separadamente a la misma portadora que tiene frecuencia de wt pero con desfase de 90°. Esto se indica
en el diagrama bajo las funciones de coseno y seno. Las señales son sumadas por
un circuito analógico lineal y de ahí al equipo transmisor. En el caso de las
normas de televisión cromática NTSC y PAL,
estas señales incorporan los pulsos de sincronización y el audio en el
transmisor, con lo cual se completa la señal televisiva. Dichos pulsos permiten
mantener la sincronización, tanto en fase como en frecuencia, entre la señal
portadora y la señal del oscilador local del receptor.
Modulador digital: El flujo de datos que proviene de la fuente S se divide en dos
partes, mediante un convertidor serie-paralelo, las cuales atraviesan dos
convertidores digital-analógico. Las señales
pasan después por filtros pasa-bajo (LPF) y luego son multiplicadas por la
misma portadora de frecuencia  , pero ésta es desfasada en 90° en una de las ramas de la figura, tal
como ocurre en la QAM Analógica. Este paso genera las señales I(t) y Q(t) que
serán transmitidas. Ambas señales son sumadas linealmente y se envían al canal
de transmisión. La señal enviada, se expresa como esta sumatoria:
, pero ésta es desfasada en 90° en una de las ramas de la figura, tal
como ocurre en la QAM Analógica. Este paso genera las señales I(t) y Q(t) que
serán transmitidas. Ambas señales son sumadas linealmente y se envían al canal
de transmisión. La señal enviada, se expresa como esta sumatoria:
Demodulador analógico: La señal analógica recibida r(t) es dividida y cada parte es enviada a dos demoduladores de
producto que la multiplican por la señal portadora con diferencias de fase de
90°. Las señales de salida de los demoduladores, denominadas Ir(t) y Qr(t) atraviesan los
filtros pasabajos TP, adecuadamente diseñados para obtener las señales finales I(t) y Q(t), que serán procesadas en forma independiente. Para mantener
la sincronización, puede existir una etapa de recuperación de portadora que
luego es filtrada y amplificada para ser mezclada o también, en forma alterna,
un lazo de seguimiento de fase. El
esquema de demodulación básico es mostrado en el diagrama que sigue.
Demodulador digital: La estructura del demodulador ideal para QAM Cuantificada o
digital se muestra seguidamente con Hr como la respuesta en
frecuencia de los filtros del sistema:
La señal r(t) se divide en dos vías, en
cada una de las cuales es multiplicada por la señal de un oscilador local con
frecuencia Fo y desfase de 90° en una de
ellas. Las señales atraviesan los filtros pasa-bajos y de allí se dirigen a dos
convertidores analógico a digital que son usados como paso previo antes de
mezclar los flujos digitales de datos en un convertidor paralelo a serie.
7.4 FSK: Modulación digital de frecuencia
Consiste en variar la frecuencia de la portadora de acuerdo a los datos. Si la fase de la señal FSK es continua, es decir entre un bit y el siguiente la fase de la sinusoide no presenta discontinuidades, a la modulación se le da el nombre de CPFSK (Continuous Phase FSK) y será la que analizaremos a continuación.
La siguiente figura ilustra un mensaje y la señal FSK resultante. Se observa que para el “1”lógico y para el “0” las frecuencias de los sinusoides son diferentes.
Las dos frecuencias involucradas las llamaremos fA y fB, y se encontraran alrededor de la frecuencia de la portadora (fc) de acuerdo a las siguientes relaciones
De esta forma:
La ecuación que defina la señal modulada en FSK sería
Entonces tenemos que si b(t) = 1:
La Densidad espectral de potencia de la señal FSK puede obtenerse modelándola como la suma de dos señales OOK de frecuencias fA y fB
Se muestra a continuación solo el lado positivo de la DEP
El ancho de banda total de la señal es:
Otra condición que generalmente se aplica es que las dos frecuencias sean ortogonales en un intervalo tb. Es decir:
Si se elige la frecuencia de portadora de manera que en un intervalo de tiempo igual a tb quepa un número entero de períodos (es decir ntc=tb=(n/fc=tb ) entonces 4π fc tb=4πn; esto implica anular la primera de las dos integrales. Para anular la otra se debe cumplir que
Si se cumple esta condición entonces las dos señales son ortogonales en el intervalo tb. La constelación de la señal FSK ortogonal se construye luego de definir las bases ortonormales






















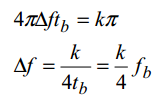

No hay comentarios:
Publicar un comentario